(1998.7.19)

1. デマンドバス

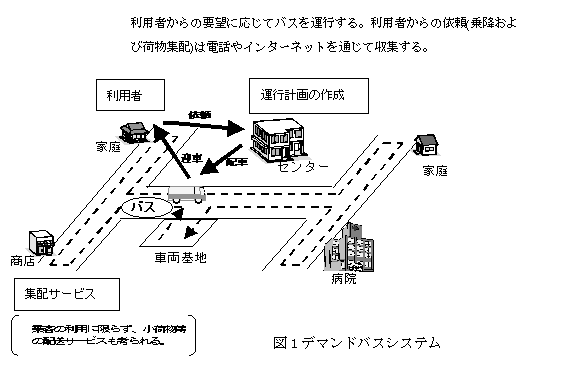
デマンドバスとは、ある定められた地域（コミュニティ）内における乗降車依頼に対し車両基地(depot)に配備されているバスによる相乗り方式のサービスをおこなうシステムをいう。デマンドバス運行管理問題（スケジューリング）とは、乗降車依頼に対する車両の割り当てとバスの巡回経路とを決める問題である。一般には、依頼後数分から３０分以内に小型バスが家の前まで向かえにきて、降車はコミュニティ内の任意の場所で可能である。バスの巡回路としてコミュニティ内を十分にカバーする道路網を想定し、前もって乗降場所を定めておく場合もある。このときはもよりの乗降場を指定する。また、あらかじめ基本運行経路を定めておき乗降要求の発生状況によりバスの運行時間を調節するという方式もある。バスはある一定の時間間隔（たとえば１５分）の間に乗車を予約してきた利用者を乗降車させながらコミュニティ内を巡回して車両基地に戻ってくる。運行管理の目的は、車両の総運行コストを小さくすることと乗客の目的地点までの所用時間を短くすることである。

2. 車両配送問題

ここでは、デマンドバスのスケジューリングを考えるために、関連する幾つかの問題について解説する

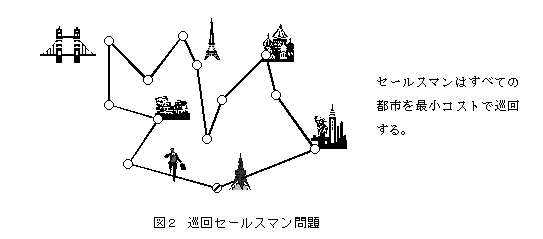
2-1. 巡回セールスマン問題（Traveling Salesman Problem, TSP）：図２のように、ｎ個の訪問すべき都市が与えられたとき、それらの都市をすべて訪れる最小コストの巡回路を見つけよという古典的な問題である。

巡回セールスマン問題は一見すると簡単な問題のように思われるが実はそうではない。この問題は理論的にはＮＰ困難問題と呼ばれる問題であり、効率よく最適解を見つけることはできない。ＮＰ困難問題というのは、直感的にいえば、基本的には総当たりの方法でしか最適解を見つけることができない問題である。ｎ個の都市を巡回する仕方はｎ！種類あるから、総当たりですべての巡回路を調べる方法では、ｎが大きくなると現在のコンピュータでは手におえなくなる。たとえば、現在のスーパーコンピュータより高速のコンピュータ（1 GFLOPS）で計算しても、ｎ=２０のときで計算時間は約８０年になってしまう。したがって、巡回セールスマン問題に対しては、正確な最適解を求めることはあきらめ、精度のよい近似解を高速に求めることが現実的な解法となる。

巡回セールスマン問題の歴史は古く、これまでにいろいろな近似解法が提案されている。最近では、4,000都市規模の場合でも誤差数％の近似解が求められるようになっている[1]。重要なことは、デマンドバス問題を含め、他の車両配送問題はすべて巡回セールスマン問題をより複雑にした問題であるということである。したがって、これらの問題も最適解を求めることはあきらめ近似解を求める効率のよい解法を探らなければならない。

2-2. 車両配送問題(Vehicle Routing Problem, VRP)：地域内のｎ個所で荷物の集荷要求があるとき、集荷基地に待機しているｋ台のトラックですべての地点を回って集荷するのに各トラックをどのようなルートで走らせるかという問題である。目的はトラックの走行距離の総和を最小にすることである。集荷作業の終了時間に制限がつく場合もある。また、トラックの積み荷が容量いっぱいになったときには集荷基地にもどらなければならない。トラックの台数が１でその容量と終了時間に制限がない場合は巡回セールスマン問題と同じ問題になる。

2-3. Pick-up and Delivery問題：車両配送問題で、地域内の要求が荷物の配達要求の場合である。各トラックは配達要求のあった地点で荷物を受け取りそれを配達先に届ける。すべての要求地点（荷物の受け取り地点と配達地点）を訪れるのは車両配送問題と同じであるが、違うのは荷物の受け取り地点に先に立ち寄らなければならないことである。荷物の配達先がすべて車両基地の場合は車両配送問題と一致する。

2-4. Dial-a-Ride問題：この問題はまさに上で述べたデマンドバスのスケジューリング問題である。Pick-up and Delivery問題と違うのは、乗客の待ち時間やバスに乗っている時間をできるだけ短くするという条件が付くことである。

車両配送問題で、各要求が集荷時間帯や配達時間帯を指定できる場合を「時間枠つき配送問題(VRP with time window, VRPTW)」という。各トラックはこれらの各要求地点にその要求で指定される時間帯の間に到着しなければならない。デマンドバス問題も、各乗客が乗車希望時間と目的地到着の希望時間を指定する場合には時間枠つき配送問題と考えることができる。

3. モデル化

コンピュータによる最適運行管理を行なうために、デマンドバス運行管理問題を数理的にモデル化する。

モデル化にあたっては、デマンドバスの様々な運行形態に応用できるような一般化された柔軟なモデルを目指す。たとえば、乗降場所はどの利用者からも数分で行けるような場所を想定しているが、道路網の拡張や新たな乗降場が生じた場合もその組み込みが容易に行なえるようにする。また、高齢者や障害者の場合には自宅前までの出迎えが望ましいが、やむをえず乗降場を利用する場合はそこへの移動時間が個別に異なると思われるので、それぞれの事情に応じてバスの出迎え時刻を指定できるようにする。また、バスターミナルでの幹線バスへの乗り換え時間や病院での診療予約時間に間に合わせるためには許容到着時間を指定できることが必要である。車イス利用者の場合にはリフト付きバスを割り当てる必要があるであろう。また、１台のバスへの乗客定員数（車イスの場合はその台数制限）を満たすようなスケジュールが必要となる。以下のモデル化ではこれらのことを組み込むことが容易にできる。

3-1. バスが一台の場合

記号の説明：

Q: バスの乗車定員

t_ij: i地点からj地点まで直行するときの所用時間（i地点での乗車時間を含む)

c_ij: i地点からj地点までの運行コスト

[a_i,b_i]: 乗降要求iの乗車（または降車）希望時間帯

X_ij: バスがi地点からj地点へ直行するときに1、そうでないとき0となる変数

T_i: i地点への到着時間を表す変数

L_i: i地点で乗降終了時のバスの乗客数

初期状態としてバスは車両基地dにある。すなわち、L_d=0,a_d=b_d=T_dとする。

以上の準備のもとでデマンドバスの運行管理問題を次のように最適化問題として定式化する。

subject to

(1)〜(5)式はいわゆる割り当て問題(assignment problem)と同じ構造である。(2)〜(5)式はネットワークの各点から出て各点に入るフローがただ一つ（つまり、バスが1台）であることを表している。(6)式はi地点からj地点へは所用時間t_ijが必要であることを表している。また、バスが早めに到着するのはかまわないことも表している。(7)式は各地点への到着時間が乗客の要求を満たすことを表している。(8)〜(11)式は各地点での乗降者数に矛盾がないための条件とバスの定員による条件である。(12)式は各乗客の乗車時間と降車時間に矛盾がないための条件である。

上の目的関数は、乗客の希望到着時間内にバスを運行したときの運行コストの最小化を考えた場合である。希望到着時刻を少し遅れてもよいが、できるだけ希望時間内におさまるようにしたい場合は(6)式と(7)式をはずし、希望到着時間とバスの到着時間の差をペナルティとして目的関数に組み込むことが可能である。

バスが1台の場合の最適運行スケジュールをコンピュータで計算する方式としては、Dumas[2]らにより一種の動的計画法を用いる方法が報告されている。その報告によれば、CYBER173計算機上で乗客40人の要求に対し6秒以下で解を求めることができた。また遺伝的アルゴリズム(GA）を用いた解法も提案されている[8]。

3-2.バスが複数台の場合

記号の説明：

前節の記号をもとにして用いる。運行可能なバスの集合をKとする。バスk(∈ K)に関するネットワークを(V^k,A^k)とする。V^k=N∪{o(k), d(k)}は頂点集合で、o(k),d(k)はそれぞれバスkの出発基地と到着基地である。A^k(⊂V^k×V^k)は枝集合である。初期状態として、どのバスkも指定時刻に車両基地を出発するものとする。つまり、T^k _o(k)=a _o(k)=b _o(k)である。

subject to

上の目的関数でc^k(L_i^k)は、バスの混み具合などの乗客へのサービス度を表すコストである。つまり、できるだけ運行コストが小さく、しかも乗客へのサービス度の高い運行スケジュールを得ようというものである。上のような定式化のもとでこの問題を解く手法についての研究は、まだ始まったばかりである。分枝限定法による探索木にDanzig-Wolfe分解を用いたアプローチを組み込んだ方法がDumas[4]らによって報告されている。また、バスが２台の場合に遺伝的アルゴリズムを用いた解法が提案されている[9]。

3-3. 運行経路が定まっている場合

バスの運行経路が定まっている場合を考える。これは、上の方法でバスの運行経路が求められたとしてもよいし、また、経営的または行政的判断などなんらかの方法で決められた場合でもよい。このとき、乗客の満足度をできるだけ大きくする（つまり不満度を小さくする）運行スケジュールを求めることを考える。乗客は乗車（または降車）希望時間帯の間にバスが到着すると満足し、バスの到着が希望時間帯をはずれるほど不満が増すとする。

subject to

不満度関数f_i(T_i)：上の定式化では、定まった経路で運行するときの乗客の不満度ができるだけ小さくなるようなバスの運行時間スケジュールを求めている。これまで、次のようなf_i(T_i)について研究がある。

1. f_i(t) = c(b_i-t)(cは定数)の場合がSexton and Bodin[6]によって調べられている。ただし、t∈(-∞,b_i]である。この定義では乗客は時刻b_iにバスが到着することを希望し、それより早くバスが到着する場合にはその時間差に比例して不満度が増す。

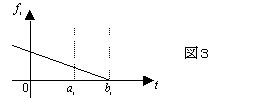
(2)

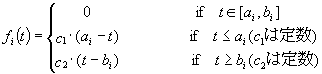
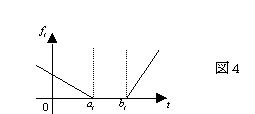
これはSexton and Choi[7]によって調べられたものである。（この場合は(28)式の条件を削除する問題である）この定義では、乗客の希望乗車（または降車）時間帯[a_i,b_i]内にバスが到着すれば乗客の不満度は0で、時刻a_iより以前（又は時刻b_iより以降）にバスが到着するときは、予定時間から離れるほど不満度が比例して増加する。

(3) f_i(t)が[a_i,b_i]上で定まる一般的な凸関数の場合がDumas[3]らによって調べられている。

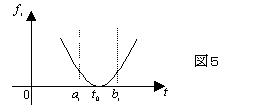
とすると、f_i(t)は時刻t₀で最小値を与える。つまり乗客は時刻t₀にバスが到着すれば不満度が0で、その時刻を外れると不満度は増加する。

4. スケジューリングの手法

ここでは、デマンドバスの最適運行スケジュールを求めるために用いられる手法について解説する。２章で述べたようにこの問題はNP困難問題であり、良い近似解を求めるアルゴリズムを設計する必要がある。このような離散最適化問題の近似解を求める方法としては、最近、以下に紹介するようなメタヒューリスティックスと呼ばれる各種手法が開発されている。実際には、対象とする問題の特性を考慮してこれらの手法から幾つかを組み合わせて性能の良いアルゴリズムを設計することになる。

(1) ローカルサーチ(Local Search)

最適化問題において、解ではあるが最適性は保証されていないものを可能解(feasible solution)という。最適化問題は可能解の集合の中から最適な解を見つけ出す問題である。たとえば、巡回セールスマン問題ではすべての可能な巡回路（ｎ！個ある）を可能解と考えればよい。可能解の集合を解空間という。ローカルサーチ（局所探索または山登り法ともいう）は次のようにして最適解を求めようとする手法である。適当な可能解をひとつ選びそれを暫定解ｓとする。解空間の中でｓの近傍の中にｓより良い解を見つけたらそれをｓと置き換える。これを繰り返し、ｓの近傍中にｓよりよい解が見つからなくなったらｓを出力する。

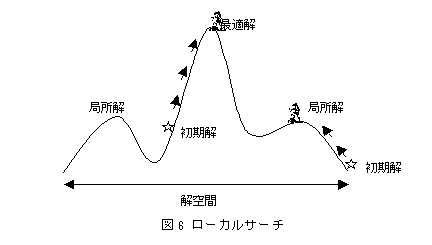
ローカルサーチでは初期解の選びかたにより真の最適解が選られる場合とそうでない場合がある。前者の解を大域最適解(globally optimal solution) と呼び、後者の解を局所最適解(locally optimal solution) と呼ぶこともある。また、近傍をどのように定めるかも解探索の性能に影響する。現在の解ｓからみてもっとも急に登る方向に歩を進めるというのは合理的と思われるが、そのような方法は一般的には最急降下法と呼ばれる。ニューロネットワークのバックプロパゲーション法による解探索などはその原理による。問題によってはローカルサーチで最適解が求まる場合もある。たとえば、線形計画問題に対するシンプレックス法は、その構造はローカルサーチであるが最適解を見つけることが保証される。また、離散構造を有する問題でも、最短路問題(shortest path problem)や最小木問題(minimum spanning tree problem)などはローカルサーチで最適解を見つけることができる。（一般的には、マトロイド構造を持つ問題は解空間に単峰性が保証されるためローカルサーチで最適解を見つけることが可能である。）ローカルサーチはその構造が非常に単純であり、以下で述べる他の探索法の基本となる。

(2) シミュレーテッドアニーリング(Simulated Annealing)

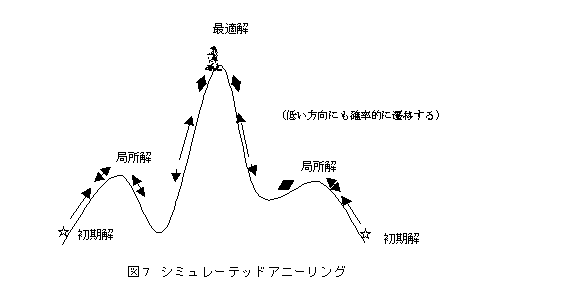
ローカルサーチの欠点は、初期解の選びかたによっては低い山の山頂に到着してしまい、得られる局所解が大域最適解に比べてそれほどよい解でない場合があることである。そこで、途中の解ｓの近傍でｓより良い解に移行するだけでなく、ｓより悪い解の方向にも確率的に遷移するということを考える。つまり、ある確率で現在地点よりも低い地点に動いてみるわけである。そのようにすることで、低い山の山頂にトラップされることが回避され、他のより高い山を目指すことが可能になる。どの程度の確率で遷移するかを定めるパラメータを温度Tで表す。最初は温度を高くしてこの遷移確率を高くしておき、最適解（または準最適解）に近づくにつれて徐々に温度を低くするといったように、Tの値をうまくコントロールして急速に最適解に近づけようとする研究が多数なされている。金属などの焼きなまし(annealing)にちなんでこの名がある。

(3) タブーサーチ(Taboo Search)

基本的にはローカルサーチであるが、局所最適解に至ってもそこでトラップされずにさらに動き回るような探索を考える。そのようにすることでより良い解に出くわす可能性が高くなる。局所最適解の地点から下り勾配の小さい方向へ下がってみるというのが基本方針である。そのように動き回ると一度辿ったところをぐるぐる回る恐れがある。これを防ぐために、一度辿った場所を記憶しておくのがタブーリストである。一度辿ったところはタブー(taboo, tabu とも綴る) であるとして二度と訪れないようにするのがこの名の由来である。

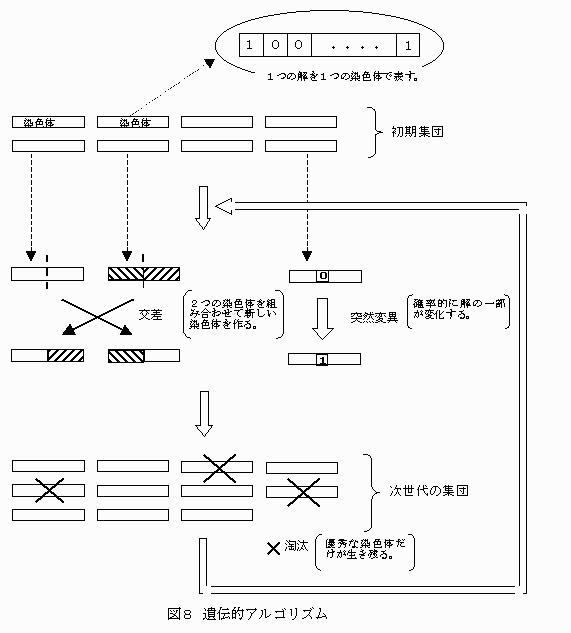
(4) 遺伝的アルゴリズム(Genetic Algorithm, GA)

生物は、その遺伝機能によって進化と環境への適応を可能にしているが、その進化過程を模倣して最適解（準最適解）を求めようとする手法である。可能解を文字列で表したものを染色体と呼び、複数の染色体を初期解の集団とする。二つの染色体を掛け合わせて新しい染色体を作ることを交差という。また、確率的に染色体の一部を置き換えることを突然変異という。これらの操作により生じた染色体のうち（環境に適応する）優秀なものだけを残し、次の世代の染色体集団を形成する。これを繰り返すことで、よい解のみを含む染色体集団を得ようというのが遺伝的アルゴリズムである。

参考文献

[1] 岩野和生、巡回セールスマン問題をめぐる最近の話題、電子情報通信学会誌 , Vol.78, No.10, pp.1045-1047(1995).

[2] J., Y. Dumas and F. Soumis, A dynamic programming solution of the large-scale single-vehicledial-a-ride problem with time windows, Am. J. Math. Manage. Sci. 6,301-325(1986).

[3] Dumas, Y., F. Soumis and J. Desrosiers, Optimizing the schedule for a fixed vehicle path with convex inconvenience costs, Transp. Sci. 24,145-152(1990).

[4] Dumas,Y., J. Desrosiers and F. Soumis, The pick-up and delivery problem with time windows, Eur. J. Oper. Res. 54, 7-22(1991).

[5] Sexton, T. and L. Bodin, Optimizing single vehicl many-to-many operations with desired delivery times: I. Scheduling, Transp. Sci. 19, 378-410(1985).

[6] Sexton, T. and L. Bodin, Optimizing single vehicl many-to-many operations with desired delivery times: II. Routing, Transp. Sci. 19, 411-435(1985).

[7] Sexton, T. and Y. Choi, Pickup and delivery of partial loads with time window, Am. J. Math. Manage. Sci. 6, 369-398(1986).

[8] 内村圭一、斉藤隆司、Hiro Takahashi, 遺伝的アルゴリズムによる乗客輸送の最適化、電学論(D), 117-D, 7,891-897(1997).

[9] 内村圭一、斉藤隆司、Hiro Takahashi, 公共交通サービスにおけるDial-a-Ride問題, 信学論、J81-A, 4,599-606(1998).

[10] Van der Bruggen, L.J.J., J.K.lenstra and P.C. Schuur, Variable-depth search for the single-vehicle pickup and delivery problem with time windows, Transp. Sci. 27, 298-311(1993).

[11] Wilson, H., and N. Colvin, Computer control of the rochster dial-a-ride system, Report R77-31, Dept. of Civil Engineering, M.I.T., Boston, Mass(1977).

[12] Wilson, H., and H. Weissberg, Advanced dial-a-ride algorithm research project:Final report, Report R76-20, Dept. of Civil Engineering, M.I.T., Boston, Mass(1976).

[13] Wilson, H., J. Sussman, H. Wang and B. Higgonet, Scheduling algorithms for a dial-a-ride systems, Urban systems Laboratory,Report USL TR-70-13, M.I.T., Boston, Mass(1971).

[14] 離散構造とアルゴリズムIV、室田一雄編、近代科学 社(1995).